Berkeley Bound

This past Sunday was the day I had thought would never come, and was simultaneously subconsciously dreading: move in day for UC Berkeley. Don’t get me wrong, I’m super excited to be here at Cal. I’m also super NOT excited to only get to see my family every couple months. Apparently I was much more attached to my family than I realized which is definitely not a bad thing as it means that they raised me right.

Right now the transition to becoming a “grown-up” has been a little rough without my parents directly behind me, always having my back. But I do know that things will get better once I adjust and I’m sure that I’ll have an awesome freshman year and maybe even be a bit sad to leave Berkeley come next summer.

Tomorrow is my first day of class so that means I’ll get to sit in on my first chemistry lecture! Yay (or not yay, I can’t tell yet)! Hopefully all goes well and I conquer Berkeley chemistry rather than have it conquer me. It’s always best to be positive.

This was a super short post, but it’s just an update to how my life is going and a note to suggest that many more chemistry posts will be coming as I delve into General Chemistry at Berkeley.

Go Bears!

Chemistry Thoughts: The Relationship Between Volume and Pressure

The countdown has begun. It’s currently T minus 7 days till I head off to Berkeley, but today is exactly the day that my chemistry panic has set in! UC Berkeley has notoriously difficult classes but the course I’ve heard about the most by far has been Chemistry 1A/1AL. Of course this means that’s the exact course I have to take my first semester in order to satisfy some requirements for medical school and my actual major.

On the bright side, I can get in a little review before I go to my first chemistry class so I don’t have a panic attack in the lecture hall, so here we go…

Boyle Oh Boyle, This Is Going To Be Good!

The most fundamental relationship between volume and pressure is illustrated through Boyle’s Law. The law is written down in several convertible forms, but we will consider it in the elementary format:

pv = C 

*p = pressure, v= volume, C= constant

The reason I chose the format pv = C is that it clearly displays the inverse relationship that pressure and volume have with one another. In mathematics, an inverse equation is shown as y = k/x, where k is a constant. Similarly, if we take the formula for Boyle’s Law and manipulate it by dividing the constant C by volume v, we will get the equation p = C/v. It’s an inverse function!

The inverse relationship means that if volume were to increase, pressure would decrease, and vice versa. Or, if pressure were to increase, volume would decrease, and once again vice versa!

If you think about it, this makes a lot of sense. Imagine a box that houses some gas, let’s say hydrogen.

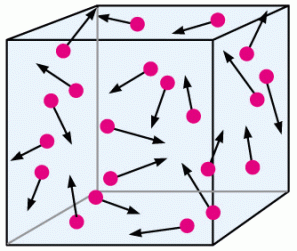
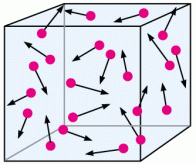
If we were to decrease the size of the box, meaning that we are decreasing the volume without changing the number of particles, then there is less space for the particles to move around without colliding. Pressure is determined by the number and force of collisions so more collisions from having less volume means greater pressure!

Changing volume in the opposite direction would work as well.

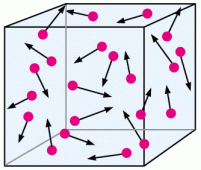
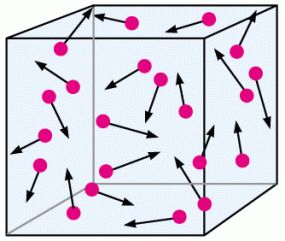
If we were to increase the size of the box, meaning that we are increasing the volume without changing the number of particles, then there is more space for the particles to move around without colliding. Less collisions therefore equates to less pressure overall!

 

This is the basic point that Boyle’s Law makes but the applications, in my opinion, go so much farther than this. Hopefully if I understand this fundamental point, I’ll understand the math involved in Berkeley’s chemistry program! Thanks Charles Boyle!

 

 

 

 

 

Don’t Count Your Acceptances Before They’ve Come

As a senior in high school on the threshold of college acceptances (or rejections?), the question of the moment is undoubtedly “where are you going to college?” It’s safe to say that this question is directed at me at least once per day, if not more, and that I have absolutely no idea how to answer it. Where am I going to college?

With university admissions becoming more and more competitive, it’s no surprise that students across the nation are placing less faith in their academic and extracurricular qualifications, no matter how impressive they may seem. The declining admissions rates for top-ranking universities ensure students that there is no absolute certainty about the likelihood of their being admitted to the schools of their choice. This uncertainty has led to the great increase in applications submitted by individual students. In my twenty-student high school English course alone, I know at least two peers who are applying to over twenty universities due to fear of not being admitted at any institution.

And it is with good reason that they fear rejection from their dream schools: Harvard College’s undergraduate admissions rate for the class of 2019 was a record-low with only 5.3% of applicants accepted. Yale University, with a slightly larger admissions rate than Harvard, welcomed a whopping 6.5% of applicants to its prestigious facility. Universities claim that dwindling acceptance rates are due to larger influxes of undergraduate applications, but the suggestion that a larger applicant pool precipitates more rejections for prospective students predicts a grave future for higher-level education in America.

The United States appears to be heading on a trajectory towards the competitive educational characteristics of European countries where only select middle school students are admitted to high school. Yes, in countries like Romania, some 14 or 15 year-olds are forced to accept trade school as an alternative to high school. While high school is mandatory for all teenagers in the U.S., the declining possibility for gifted students to enroll in Ivy League or other comparable institutions parallels the lack of opportunity in the Romanian education system. My own mother, now a successful Treasury Accountant at a notable law firm, was forced to opt out of university in Romania due to her lacking physics exam score and went to work immediately after graduating from high school. It was only when she came to America that she was able to enroll in college courses and pursue a career in accounting.

If the United States were to become a country where intelligent students are forced to develop their education at universities that are unable to challenge them intellectually, the very heart of progress would be diminished. Students are told to aim for universities where they will neither be too comfortable with the courses nor challenged too greatly for their academic capacity. Yet, when many qualified teenagers are being rejected from schools that suit their abilities, there seems to be some sort of hypocrisy.

I guess the only thing that is safe to say now is that America will once again get a glimpse of its educational future come March when admissions decisions roll out.