The countdown has begun. It’s currently T minus 7 days till I head off to Berkeley, but today is exactly the day that my chemistry panic has set in! UC Berkeley has notoriously difficult classes but the course I’ve heard about the most by far has been Chemistry 1A/1AL. Of course this means that’s the exact course I have to take my first semester in order to satisfy some requirements for medical school and my actual major.
On the bright side, I can get in a little review before I go to my first chemistry class so I don’t have a panic attack in the lecture hall, so here we go…
Boyle Oh Boyle, This Is Going To Be Good!

The most fundamental relationship between volume and pressure is illustrated through Boyle’s Law. The law is written down in several convertible forms, but we will consider it in the elementary format:
pv = C
*p = pressure, v= volume, C= constant
The reason I chose the format pv = C is that it clearly displays the inverse relationship that pressure and volume have with one another. In mathematics, an inverse equation is shown as y = k/x, where k is a constant. Similarly, if we take the formula for Boyle’s Law and manipulate it by dividing the constant C by volume v, we will get the equation p = C/v. It’s an inverse function!
The inverse relationship means that if volume were to increase, pressure would decrease, and vice versa. Or, if pressure were to increase, volume would decrease, and once again vice versa!
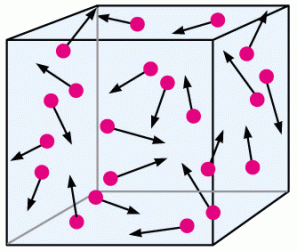
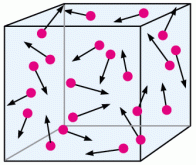
If you think about it, this makes a lot of sense. Imagine a box that houses some gas, let’s say hydrogen.
If we were to decrease the size of the box, meaning that we are decreasing the volume without changing the number of particles, then there is less space for the particles to move around without colliding. Pressure is determined by the number and force of collisions so more collisions from having less volume means greater pressure!
Changing volume in the opposite direction would work as well.
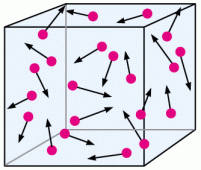

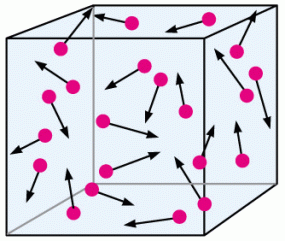
If we were to increase the size of the box, meaning that we are increasing the volume without changing the number of particles, then there is more space for the particles to move around without colliding. Less collisions therefore equates to less pressure overall!
This is the basic point that Boyle’s Law makes but the applications, in my opinion, go so much farther than this. Hopefully if I understand this fundamental point, I’ll understand the math involved in Berkeley’s chemistry program! Thanks Charles Boyle!